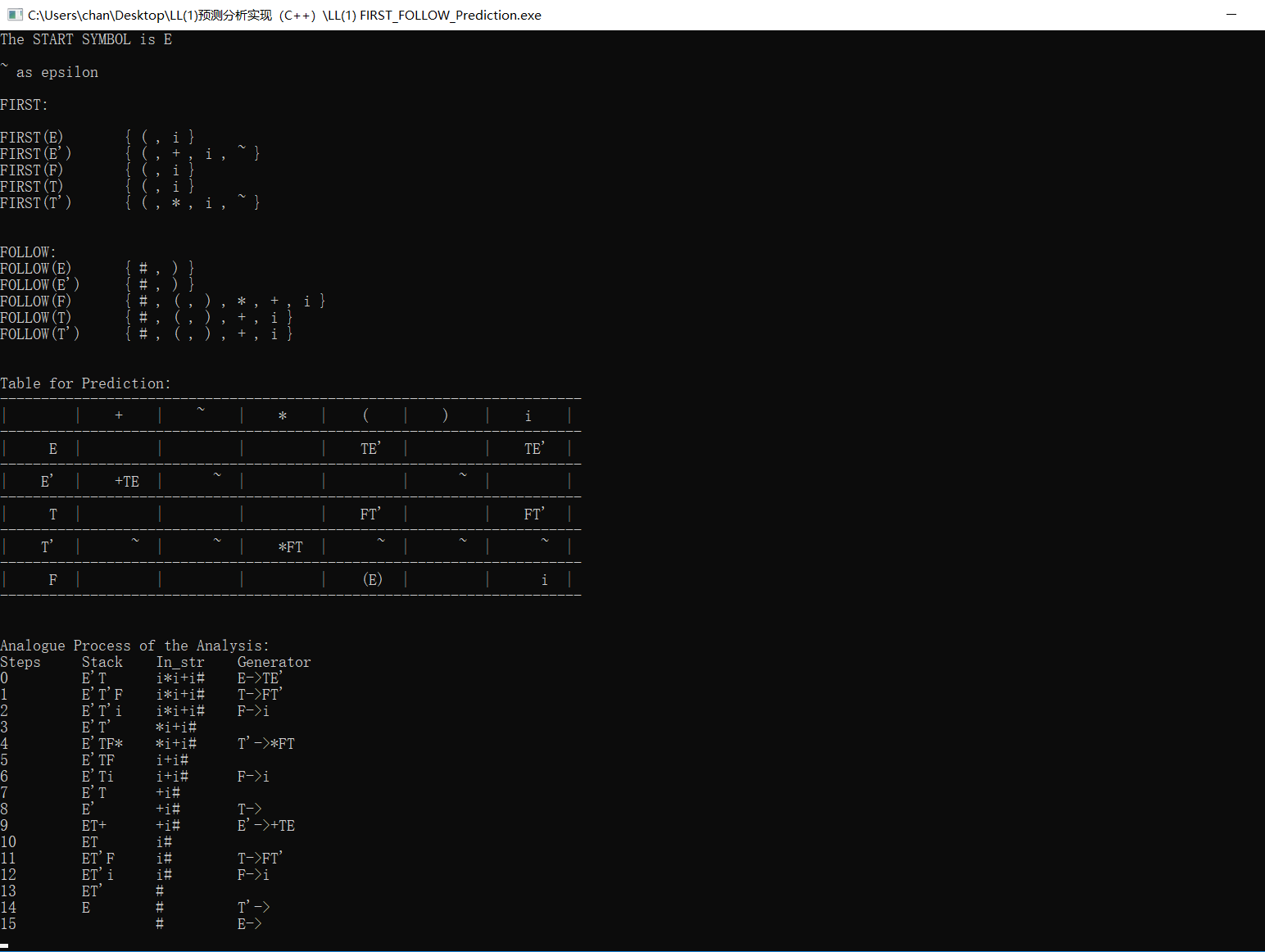
输入函数和数据结构
所用数据结构:
FIRST集和FOLLOW集均为从string到char集合的映射(考虑到存在非终结符如E’,而终结符均为小写字母)
S初始化为空串,可以自定义,但是如果未定义则调用缺省规则:将会选取出现在文件中的第一条产生式的非终结符。
Atom_Re : 定义了一个类为atom_relation,可看作为用类似十字链表存储的图,表示的是生成式左部和右部的关系。对于每个Atom_Re,它的 $.left$ 是唯一的,对应文法的一个左部,而其对应的右部则会全部出现在这个类的 $.right$ 中。
VN_dic: $string$ 到 $int$ 的映射,记录了每一个非终结符(在这里是$string$容器)的唯一编号,以便生成Atom_Re类
VN_set: 注意并不是$set$容器,而是$vector$容器,但是其元素也是$unique$的(利用VN_dic保存的序号维护)。
eps: 初始化了一个常量$string$ 保存epsilon字符设置(使用$string$以便与$char$数据格式兼容,实际使用取容器的 $*begin()$ 或$[0]$即可)
map<string,set<char> > first;
map<string,set<char> > follow;
string S="";
const string eps="~";
vector<Atom_Re> VN_set;
map<string,int> VN_dic;
class Atom_Re
{
public:
string left;
set<string> right;
Atom_Re(string ipt)
{
left=ipt;
}
void isrt(string rt)
{
right.insert(rt);
}
void debug_print()
{
cout<<"Left Part : "<<left<<" Right Part: ";
if(!right.empty())
{
if(right.size()==1)
{
cout<<*right.begin();
}
else
{
auto it=right.begin();
cout<<*it;
for(; it!=right.end(); ++it)
{
cout<<"|"<<*it;
}
}
cout<<endl;
}
else
cout<<"OOPS!It is empty here.\n";
}
};
输入函数:
void input(int& n)
{
cin>>n;
string tmp;
VT.insert('#');
for(int times=0; times<n; times++)
{
cin>>tmp;
string LEFT="";
string RIGHT="";
auto it=tmp.begin();
for(; it!=tmp.end(); ++it)
{
if(*it=='-')
break;
LEFT+=*it;
if(*it!='\''&&!isupper(*it)&&*it!=eps[0])
{
VT.insert(*it);
}
}
++it;
++it;
if(times==0)
{
if(S=="") //default config
S=LEFT;
cout<<"The START SYMBOL is "<<S<<endl<<endl;
}
if(!VN_dic[LEFT])
{
VN_set.push_back (LEFT);
//cout<<LEFT<<endl;
VN_dic[LEFT] = VN_set.size();
}
for(; it!=tmp.end(); ++it)
{
if(*it!='\''&&!isupper(*it)&&*it!=eps[0])
{
VT.insert(*it);
}
RIGHT+=*it;
}
VN_set[VN_dic[LEFT]-1].isrt(RIGHT);
//cout<<RIGHT<<endl;
}
}
FIRST 和 FOLLOW
Definition:
FIRST($\alpha$)是可从$\alpha$ 推导出的串的首符号集合,其中$\alpha$是任意的语法文法符号串。
FOLLOW(A)则是在某些句型中紧跟在A右边的终结符号的集合,其中A只能是非终结符号。
实现方法:
对于FIRST集:
-
如果$X$是终结符,FIRST($X$) = $X$
-
如果$X$ 是一个产生式,则将 $\epsilon$ 加入到FIRST($X$)中
-
如果$X$是一个非终结符,且有产生式 $X \rightarrow Y_1,Y_2…Y_k$ ,其中$k\geq1$ ,那么如果存在一个$i$,使得$a$在FIRST($Y_i$)中且$\epsilon$ 在所有的FIRST($Y_s$) 中,其中$1 \leq s \leq i-1$ ,此时将$a$加入到FIRST($X$)中。当对于所有的$j = 1,2,…,k$都有 $\epsilon \in FIRST(Y_j)$ 时 ,就将 $\epsilon$ 加入到FIRST($X$)中。
Code:
bool vis[MAX];
void DFS(int x)
{
if(vis[x]) //避免递归死循环,记录访问节点
return;
vis[x]=1;
string& left = VN_set[x].left; //取左部
set<string>& right = VN_set[x].right; //取对应的右部集合
auto it = right.begin();
for ( ; it!= right.end() ; it++ ) //遍历右部
{
for ( int i=0 ; i<it->length() ; i++ ) //对于一个右部规则
{
if(!isupper(it->at(i))&&it->at(i)!='\'') //非终结符直接插入
first[left].insert(it->at(i));
if(isupper(it->at(i)))
{
int idx=0;
if(it->at(i+1)=='\''&&i!=it->length()-1)
{
idx=VN_dic[it->substr(i,2)]-1;
}
else
{
idx=VN_dic[it->substr(i,1)]-1;
}
string nxtLeft=VN_set[idx].left; //保存左部
DFS(idx);//递归
set<char>& tmp=first[nxtLeft];//对应的子树的first集
auto sc=tmp.begin();
bool flag=0;
for(; sc!=tmp.end(); ++sc)
{
if(*sc==eps[0]) //存在epsilon,结束对于这个规则的递归
{
flag=1;
}
first[left].insert(*sc);
//否则left对应的first集可以加上叶节点对应的非终结符
}
if(flag==0)
break;
}
else
continue;
}
}
}
//IN MAKE_FIRST():
MST(vis);
for(int i=0; i<VN_set.size(); i++)
DFS(i);
对于FOLLOW集:
- 将 ’ # ’ 加入到FOLLOW($S$) 中。
- 如果有产生式:$A\rightarrow \alpha B \beta$ ,那么FIRST($\beta$)中除了$\epsilon$之外的所有符号都在FOLLOW($B$)中。
- 若存在一个产生式$A\rightarrow \alpha B$ ,或者存在一个产生式 $A\rightarrow \alpha B \beta$ 且FIRST($\beta$)包含了$\epsilon$,那么FOLLOW($A$)$\subseteq$FOLLOW($B$)。
void make_follow()
{
follow[S].insert('#'); //S的follow集中插入 # 标记
while(1)
{
bool loop_flag = false;
for ( int i=0 ; i<VN_set.size(); i++ ) //遍历VN集
{
string& left=VN_set[i].left;
set<string>&right =VN_set[i].right; //取出右部规则集合
auto it = right.begin();
for ( ; it!= right.end() ; it++ ) //遍历右部集(逆向遍历)
{
bool flag = true; //是否最右边有epsilon
const string& str = *it;
for ( int j = it->length()-1 ; j >= 0 ; j-- )
{
if ( str[j] == '\''||isupper(str[j] ) )
{
int mns=0;
if(str[j]!='\'')
mns=-1;
//一个标志位,记录是否有E'这种情况出现影响substr的parameter设置
string VN=it->substr(j-1-mns,2+mns); //读入非终结符
int x = VN_dic[VN]-1;
if ( flag )
{
int tt = follow[VN].size();
append ( left, VN ); //运用规则3,FIRST(A)并入FOLLOW(B)
int tt1 = follow[VN].size();
if ( tt1 > tt ) //有改变
loop_flag = true;
//标志位:只要有新元素加入,可以继续执行程序(定义),下同
if ( !VN_set[x].right.count(eps) )
flag = false;
}
for ( int k = j+1 ; k < it->length() ; k++ ) //向后循环遍历
{
if ( isupper(str[k]) )
{
string id;
if ( k != it->length()-1 && str[k+1] == '\'' )
id = it->substr(k,2);
else
id = it->substr(k,1); //求对应的VN(beta)
set<char>& from = first[id];
set<char>& to = follow[VN];
//运用规则2
int tt = to.size();
auto it1 = from.begin();
for ( ; it1 != from.end() ; it1++ )
if ( *it1 != eps[0] )
to.insert ( *it1 );
int tt1 = follow[VN].size();
if ( tt1 > tt )
loop_flag = true;
if ( !VN_set[VN_dic[id]-1].right.count("~") )
break;
//如果(beta)右部即FIRST(beta)有epsilon,终止循环
}
else if ( str[k] != '\'' ) //若为终结符
{
int tt = follow[VN].size();
follow[VN].insert ( str[k] );//直接加入
int tt1 = follow[VN].size();
if ( tt1 > tt )
loop_flag = true;
break;
}
else
continue;
}
if(str[j]=='\'') //若为',注意迭代器需继续回退
j--;
}
else
flag=0;
}
}
}
if(!loop_flag)
break;
}
//OUTPUT FUNC:...........
//.........................
}
生成预测分析表
数据结构
$predict_table$ : 内层的$map$是终结符到生成式,而$vector$容器的元素顺序和$VN_set$ 的顺序一样。
vector<map<char,string> > predict_table;
vector<char> letter;
方法:
对于文法 $G$ 的每一个产生式$A->\alpha$ ,进行如下处理:
- 对于每一个FIRST($\alpha$)中的终结符号$\alpha$,将$A->\alpha$加入表$[ A , a]$
- 若$\epsilon$在FIRST($A$)中,那么对于FOLLOW($A$)中的每一个终结符号$b$,将$A->\alpha$加入到表$[ A , b]$中。如果 $\epsilon$ 在FIRST($\alpha$)中且‘$#$’在FOLLOW($A$)中,也将$A->\alpha$加入到表$[ A , #]$中。
Code:
void TABLE()
{
map<char,string> temp;
vector<char> letter;
bool vis[500]; //终结符访问数组
memset ( vis , 0 , sizeof ( vis ) );
for ( int i = 0 ; i < VN_set.size() ; i++ ) //表循环外层为列,及非终结符
{
set<string>& right = VN_set[i].right;//右部集合
set<string>::iterator it = right.begin();
for ( ; it != right.end() ; it++ ) //遍历右部
for ( int j = 0 ; j < it->length() ; j++ )
if ( !isupper(it->at(j)) && it->at(j) != '\'' )
{
if ( vis[it->at(j)] ) continue;
vis[it->at(j)] = true;
letter.push_back ( it->at(j) );
}
}
for ( int i = 0 ; i < VN_set.size() ; i++ ) //表循环外层为列,及非终结符
{
temp.clear();
string& left = VN_set[i].left;
set<string>& right = VN_set[i].right;
set<string>::iterator it = right.begin();
for ( ; it != right.end() ; it++ )
for ( int j = 0 ; j < letter.size() ; j++ )//规则1
{
//cout << *it << " " << letter[j] << endl;
if ( check_first ( *it , letter[j] ) ) //检查a出现在FIRST(alpha)中
{
//cout << "YES" << endl;
temp[letter[j]] = *it; //出现就记录alpha
}
//规则2:出现epsilon还要看FOLLOW(A)里有没有letter[j]
if ( it->at(0) == '~' && check_follow ( left, letter[j] ))
temp[letter[j]] = *it;
}
predict_table.push_back ( temp );
}
///---------------输出表----------------
cout<<"Table for Prediction:\n";
for ( int i = 0 ; i <= (letter.size()+1)*10 ; i++ )
cout<<"-";
cout<<endl;
cout<<"|";
cout<<setw(9)<<right<<"|";
for ( int i = 0 ; i < letter.size() ; i++ )
cout<<setw(5)<<right<<letter[i]<<setw(5)<<"|";
cout<<endl;
for ( int i = 0 ; i <= (letter.size()+1)*10 ; i++ )
cout<<"-";
cout<<endl;
for ( int i = 0 ; i < VN_set.size() ; i++ )
{
cout<<"|"<<right<<setw(6)<<VN_set[i].left<<internal<<setw(3)<<"|";
for ( int j = 0 ; j < letter.size() ; j ++ )
if ( predict_table[i].count(letter[j] ) )
cout<<internal<<setw(7)<<predict_table[i][letter[j]]<<internal<<setw(3)<<"|";
else cout<<right<<setw(10)<<"|";
cout<<endl;
for ( int i = 0 ; i <= (letter.size()+1)*10 ; i++ )
cout<<"-";
cout<<endl;
}
cout<<endl<<endl;
}
预测分析过程
Code:
stack<string> stk;
stk.push(S);
int steps=0;
int idx=0;
while ( !stk.empty() )
{
string u = stk.top();
string tmp=""; //初始化tmp串
stk.pop();
if (!isupper(u[0])) //终结符
{
if (idx==src.length()&&u[0]==eps[0]); //epsilon则继续
else if (src[idx]==u[0]) //相等则匹配
idx++;
}
else
{
int x=VN_dic[u]-1; //查栈顶元素对于的index
tmp=predict_table[x][src[idx]];
//查预测分析表对应的生成式(src是输入串,都是终结符)
for( int i =tmp.length()-1 ; i>=0 ;i--)
{
if ( tmp[i] == '\'' ) //E'特判
{
string v = tmp.substr(i-1,2);
stk.push ( v );
i--;
}
else
{
string v = tmp.substr(i,1);
stk.push( v );
}
}
tmp=u+"->"+tmp; //加入规则串
}
print(steps++,stk,src,tmp,idx);
}
运行效果: