总论
在算符文法中,任何两个句型都不包括两个相邻的非终结符。由此定义算符优先关系:
| 关系 | 解释 |
|---|---|
| $a=b$ | $A \rightarrow …ab…$ OR $A\rightarrow …aBb…$ |
| $a\lessdot b$ | $A \rightarrow …aB…$ AND ( $B \Rightarrow^{+}b… $ OR $B\Rightarrow^{+}Cb…$ ) |
| $a\gtrdot b$ | $A \rightarrow …Bb…$ AND ( $B \Rightarrow^{+}a… $ OR $B\Rightarrow^{+}aC…$ ) |
全局数据结构
string ipt;
map< string,set<string> > raw;
set<string> VN;
set<char> VT;
map<string,set<char>> FVT;
map<string,set<char>> LVT;
map<char,map<char,char>> prior;
vector<string> rec;
set<string> aid;
set<pair<string,string>> generator;
| Data Structure | Function |
|---|---|
| $ipt$ | 输入串 |
| $VN$ | 非终结符集合 |
| $VT$ | 终结符集合 |
| $raw$ | 以$VN$为左部的所有生成式集合 |
| $FVT$ | FIRSTVT |
| $LVT$ | LASTVT |
| $aid$ | 辅助集合,存放递归时的所有父节点对应的$VN$ |
| $generator$ | 辅助映射,记录递归时父节点中$VN$直接推出的某个生成式 |
| $prior$ | s算符优先表,双重$map$以便以字符为index调用 |
| $rec$ | 规约栈 |
构造FIRSTVT 与LASTVT
递归构造,每次注意保存生成式状态以及以及父节点所有的$VN$,同时成对释放,以免成环递归。
FIRST 和 LASTVT只需要更改几个参数和一些特判(从前往后和从后往前时,形如$E’$这种数据需要重新特判!
void FIRSTVT(string vn)
{
aid.insert(vn);
auto ans=raw[vn];
for(auto it=ans.begin(); it!=ans.end(); ++it)
{
string gen=*it;
if(generator.count(pair<string,string>(vn,gen))>0 )
continue;
generator.insert(pair<string,string>(vn,gen));
//cout<<vn<<"->"<<gen<<endl;
if(isupper(gen[0]))
{
string nxt="";
nxt+=gen[0];
if(gen[1]=='\'')
nxt+=gen[1];
for(auto & all_p : aid)
{
if(!isupper(gen[1])&&gen[1]!='\'')
{
FVT[all_p].insert(gen[1]) ;
}
else if(!isupper(gen[2])&&gen[1]=='\'')
{
FVT[all_p].insert(gen[2]) ;
}
}
FIRSTVT(nxt);
}
else
{
for(auto & all_p : aid)
FVT[all_p].insert(gen[0]) ;
}
generator.erase(pair<string,string>(vn,*it));
}
aid.erase(vn);
}
void LASTVT(string vn)
{
aid.insert(vn);
auto ans=raw[vn];
for(auto it=ans.begin(); it!=ans.end(); ++it)
{
string gen=*it;
if(generator.count(pair<string,string>(vn,gen))>0 )
continue;
generator.insert(pair<string,string>(vn,gen));
//cout<<vn<<"->"<<gen<<endl;
int len=gen.size()-1;
if(isupper(gen[len])||gen[len]=='\'')
{
string nxt="";
nxt+=gen[len];
if(gen[len]=='\'')
nxt+=gen[len-1];
for(auto & all_p : aid)
{
if(!isupper(gen[len-1])&&gen[len]!='\'')
{
LVT[all_p].insert(gen[len-1]) ;
}
else if(!isupper(gen[len-2])&&gen[len]=='\'')
{
LVT[all_p].insert(gen[len-2]) ;
}
}
LASTVT(nxt);
}
else
{
for(auto & all_p : aid)
LVT[all_p].insert(gen[gen.size()-1]) ;
}
generator.erase(pair<string,string>(vn,*it));
}
aid.erase(vn);
}
生成算符优先表
三条规则,遍历即可。
| 关系 | 生成式形如 |
|---|---|
| $a=b$ | $…aVNb…$ OR $…ab…$ |
| $a\lessdot FIRST(VN)$ | $…aVN…$ |
| $ LAST(VN)\gtrdot a$ | $…VNa…$ |
void make_table()
{
prior['#']['#']='=';
for(auto & gen : rec)
{
for(int i=0; i<gen.size(); i++)
{
if(isupper(gen[i])||gen[i]=='\'')
continue;
if(i+1<gen.size())
{
string vn="";
if(isupper(gen[i+1]))
{
vn+=gen[i+1];
if(i+2<gen.size()&&gen[i+2]=='\'')
{
vn+="\'";
}
for(auto &cc : FVT[vn])
{
prior[gen[i]][cc]='<';
}
int kop=i+2;
if(gen[i+2]=='\''&&kop<gen.size())
kop=i+3;
//if(kop<gen.size())
// cout<<gen[i]<<" "<<gen[kop]<<endl;
if( kop<gen.size() && (!isupper(gen[kop])) )
prior[gen[i]][gen[kop]]='=';
}
else
{
prior[gen[i]][gen[i+1]]='=';
}
}
if(i-1>=0)
{
string vn="";
if(isupper(gen[i-1])||gen[i-1]=='\'')
{
vn+=gen[i-1];
if(gen[i-1]=='\'')
{
vn+=gen[i-2];
}
for(auto &cc : LVT[vn])
{
prior[cc][gen[i]]='>';
}
}
}
}
}
}
移进与规约分析
留坑,二义性难解决。
运行实例
Sample为《编译原理》(清华大学出版社,王省原等,第三版)例5.3。($\uparrow $在此改为 $\vert $ )
先输入生成式数量($int$),再分行输入生成式,最后输入待分析的符号串。
9
E'->#E#
E->E+T
E->T
T->T*F
T->F
F->P|F
F->P
P->(E)
P->i
i+i#
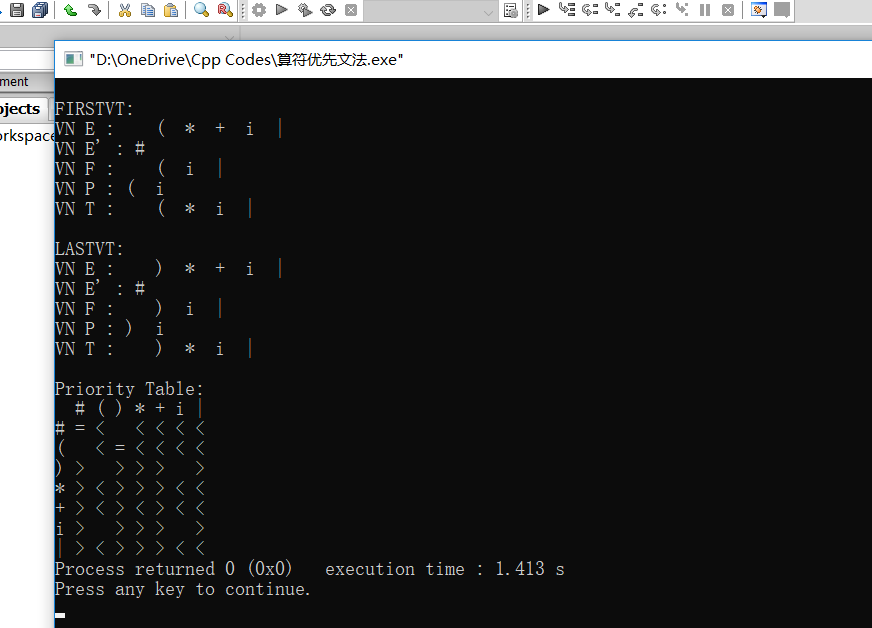
运行结果